Главная / Обучение / Теория / Обтекание тонкой пластины

1.4. Обтекание воздушным потоком тонкой пластины

Как уже говорилось, величина и направление действия аэродинамической силы зависят от формы обтекаемого тела и его ориентации в потоке. В этом разделе мы рассмотрим более подробно процесс обтекания тонкой пластины воздушным потоком и построим графики зависимости коэффициентов подъемной силы и сопротивления от угла установки пластины к потоку (угла атаки).

Если установить пластину вдоль потока (угол атаки равен нулю), обтекание будет симметричным. В этом случае поток воздуха пластиной не отклоняется и подъемная сила Y равна нулю. Сопротивление X минимально, но не нуль. Оно будет создаваться силами трения молекул воздуха о поверхность пластины. Полная аэродинамическая сила R минимальна и совпадет с силой сопротивления X как в рассмотренном ранее примере с круглым парашютом.

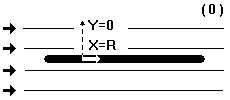
Рис. 1.23. Пластина установлена вдоль потока.
Y=0, X=R.

Начнем понемногу отклонять пластину. Из-за скашивания потока появляется подъемная сила Y. Сопротивление X немного увеличивается по причине увеличения поперечного сечения пластины по отношению к потоку.

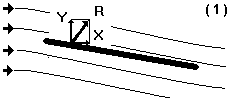
Рис. 1.24. Начало отклонения пластины.
Появилась Y, немного выросло X.

Еще немного увеличиваем угол атаки. Скос потока и подъемная сила увеличиваются. Очевидно, что сопротивление тоже растет. Заметим, что на малых углах атаки подъемная сила растет значительно быстрее, чем сопротивление.

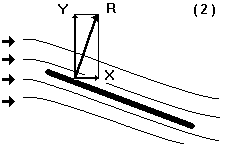
Рис. 1.25. Немного увеличиваем угол атаки.
На малых углах атаки Y растет быстрее чем X.

При продолжении увеличения угла атаки воздушному потоку становится "труднее" обтекать пластину. Подъемная сила увеличивается, но меньше, чем раньше. Сопротивление растет все быстрее и обгоняет рост подъемной силы. В результате полная аэродинамическая сила R начинает отклоняться назад.

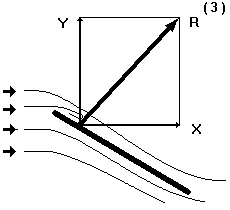
Рис. 1.26. На больших углах атаки X растет быстрее чем Y
и полная аэродинамическая сила R отклоняется назад.

Еще немного увеличиваем угол атаки, и картина обтекания радикально меняется. Воздушные струйки оказываются не в состоянии плавно обходить верхнюю поверхность пластины. За пластиной образуется мощный вихрь. Подъемная сила резко падает, сопротивление продолжает быстро увеличиваться. Это явление в аэродинамике называют "срыв потока". "Сорванное" крыло перестает быть крылом. Оно перестает лететь и начинает падать.

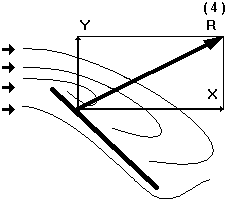
Рис. 1.27. Срыв потока. Подъемная сила резко падает,
сопротивление продолжает быстро увеличиваться.

Посмотрите зависимость коэффициентов подъемной силы C_y и сопротивления C_x от угла установки пластины к набегающему потоку (угла атаки) на графиках. При нулевом угле атаки C_y равен нулю. С увеличением угла он растет, достигает максимума в точке (3) и далее падает по причине срыва потока. Коэффициент сопротивления C_x все время растет. На малых углах атаки в области точек (0), (1) и (2) он растет относительно медленно. На больших углах, соответствующим точкам (3) и (4), значительно быстрее.

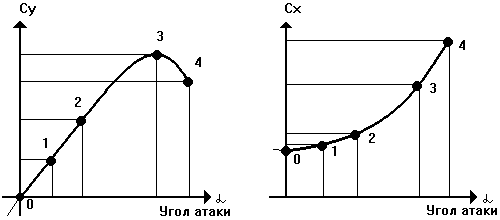
Рис. 1.28. Зависимость коэффициентов подъемной силы C_y и сопротивления C_x от угла атаки.

Объединим получившиеся два графика в один. По оси X отложим значения коэффициента сопротивления C_x, а по оси Y коэффициент подъемной силы C_y.

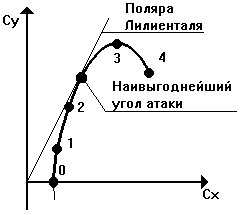
Рис. 1.29. Поляра крыла.

Получившаяся кривая называется "поляра крыла" — основной график, характеризующий летные свойства крыла. График показывает величину и направление действия полной аэродинамической силы R в зависимости от угла атаки если принять, что центр давления (точка приложения полной аэродинамической силы) находится в центре координат. На поляре можно отметить три характерные точки и соответствующие им углы атаки: критический, экономический и наивыгоднейший.

Критический угол атаки — угол атаки, при превышении которого происходит срыв потока.

На критическом углу значение С_y максимально и при выводе на него крыло сможет лететь с минимальной скоростью. Однако приближаться к этому углу следует с большой осторожностью. Превышение критического угла атаки ведет к срыву потока на крыле и потере им несущих свойств.

Как вы помните, условием прямолинейного полета с постоянной скоростью является равновесие между полной аэродинамической силой и силой тяжести. Вспомним формулу полной аэродинамической силы:

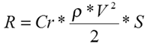
Из формулы видно, что для обеспечения постоянности итогового значения аэродинамической силы R увеличение коэффициента C_r ведет к уменьшению скорости полета V, так как значения плотности воздуха p и площади крыла S постоянны.

Экономический угол атаки — угол атаки, на котором аэродинамическое сопротивление крыла минимально.

Если установить крыло на экономический угол атаки, оно сможет лететь с максимальной скоростью.

Наивыгоднейший угол атаки — угол атаки, на котором отношение коэффициентов подъемной силы и сопротивления C_y/C_x максимально.

В этом случае угол отклонения аэродинамической силы от направления движения воздушного потока максимален. При установке крыла на наивыгоднейший угол атаки оно полетит в неподвижном воздухе дальше всего.